

Charger l'image "bronze".
On estime le gradient horizontal en calculant la valeur absolue de la différence entre l'intensité d'un pixel
et celle du pixel de droite (et ce, pour l'ensemble des pixels de l'image).
Produire l'image du gradient horizontal à l'aide d'une macro.
On utilisera en particulier les instructions AphImgGetPixel et AphImgSetPixel.
Qu'observe-t-on pour les contours horizontaux de l'image ?
On va estimer le gradient horizontal.
Sub main
AphDeferRefresh true
dim size() as long
AphImgGetSize AphImg("Bronze"), size
xSize = size(0)
ySize = size(1)
dim point(2) as long
dim x as Integer
dim y as Integer
dim g as Integer
dim g2 as Integer
AphImgCopy AphImg("Bronze"), AphImgNew("sortie")
for y = 0 to ySize-1 step 1
point(1) = y
for x = 0 to xSize-1 step 1
point(0) = x
g = AphImgGetPixel(AphImg("Bronze"),point)
point(0) = x+1
g2 = AphImgGetPixel(AphImg("Bronze"),point)
g = Abs(g - g2)
AphImgSetPixel AphImg("sortie"), point, g
next x
next y
AphDeferRefresh false
End Sub


On constate l'affichage des contours verticaux (pas de bordure horizontale), mais les contours horizontaux ont disparus.
Charger l'image "bronze".
Convoluer cette image avec le filtre horizontal (-1,1) en utilisant l'opérateur ImgConvolve,
puis retenir la valeur absolue des résultats.
Vous devriez retrouver le résultat obtenu en I.1.

Hormis un problème d'affichage lié semble-t-il au format d'image, on retrouve avec l'opérateur ImgConvolve l'extraction des contours de la question 1.
Procéder de même avec le filtre vertical (-1,1).
Combiner les deux résultats (vertical et horizontal) avec un ImgAdd.
Le problème de l'orientation subsiste-t-il ?
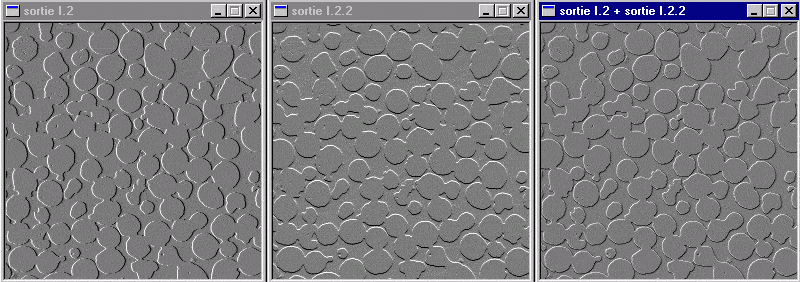
L'addition des résultats des filtres horizontaux et verticaux permet de supprimer le problème de l'orientation : les contours verticaux et horizontaux sont extraits.
Effectuer la même manipulation qu'en 2 avec l'image "clocks" (observer l'aiguille des minutes lors de l'application du filtre vertical). Discuter de la qualité du résultat.



Résultat de l'application du filtre ImgConvolve en vertical et horizontal.
L'aiguille des minutes (verticale) disparaît lors de l'application du filtre vertical.

L'addition des résultats des filtres horizontaux et verticaux permet de supprimer le problème d'effacement de l'aiguille des minutes. Le résultat obtenu est satisfaisant.
Effectuer la même manipulation qu'en 2 avec l'image "fruit".
Transformer le résultat de l'estimation du gradient en niveaux de gris
(ImgRGBToHSI, puis ImgSplitBand pour retenir la bande 2 correspondant à l'image en intensité).
Recommencer l'opération en transformant d'abord l'image en niveaux de gris et en terminant par l'estimation du gradient comme en 2.
Discuter de la qualité des deux méthodes et des deux résultats
(examiner en particulier le bord de la serviette bleue à droite de l'image).



On trouve des résultats sensiblement identiques pour la technique 1 (ci-dessus) et la technique 2 (à gauche).
La technique 1 est cependant plus longue à mettre en œuvre.
La méthode 2 (niveau de gris en premier), fait beaucoup plus ressortir le contour entre la serviette bleue et la table (bois marron).
En effet, sur l'image en couleur, ce contour n'est pas très marqué,
mais la transformation en niveau de gris a fortement marqué ce contour (le bleu est très distant du marron).
On peut donc conclure que la méthode 1 (en couleur) est plus fidèle aux contours perçus par l'œil.
Proposer un filtre 2×2 permettant de traiter en un seul passage tous les contours, qu'ils soient horizontaux ou verticaux. Justifier votre choix. Le tester.

Filtre ((-4,1)(1,2)). Résultat assez satisfaisant.
Ce filtre permet d'utiliser l'information des 4 pixels accessibles par la matrice 2x2.
Il met en évidence l'écart entre le pixel en haut à gauche (0,0) et les trois autres.
La somme des coefficients est égale à 0.
Le filtre ((-2,0)(0,2)) semble curieusement plus efficace.
Consulter l'aide en ligne relative aux opérateurs ImgRobertsEdges, ImgSobelEdges,
et ImgPrewittEdges. Proposer une macro implémentant le filtre de Sobel
(sans utiliser l'opérateur préprogrammé bien entendu...

Le résultat obtenu met bien en valeur les contours.
C'est assez différent du résultat obtenu avec le filtre de Aphelion.
|
et |
|
Sub main
AphDeferRefresh true
dim size() as long
AphImgGetSize AphImg("Fruit"), size
xSize = size(0)
ySize = size(1)
dim point(2) as long
dim x as Integer
dim y as Integer
dim g as Integer
dim somx as Integer
dim somy as Integer
AphImgCopy AphImg("Fruit"), AphImgNew("sortie")
for y = 1 to ySize-1 step 1
for x = 1 to xSize-1 step 1
somx = 0
somy = 0
point(1) = y-1
point(0) = x-1
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * 1
point(0) = x
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * 2
point(0) = x+1
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * 1
point(1) = y+1
point(0) = x-1
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * (-1)
point(0) = x
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * (-2)
point(0) = x+1
g = AphImgGetPixel(AphImg("Fruit"),point)
somx = somx + g * (-1)
point(0) = x
point(1) = y
point(0) = x-1
point(1) = y-1
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * 1
point(1) = y
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * 2
point(1) = y+1
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * 1
point(0) = x+1
point(1) = y-1
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * (-1)
point(1) = y
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * (-2)
point(1) = y+1
g = AphImgGetPixel(AphImg("Fruit"),point)
somy = somy + g * (-1)
point(0) = x
point(1) = y
AphImgSetPixel AphImg("sortie"), point, ((abs(somx) + abs(somy)) / 4)
next x
next y
AphDeferRefresh false
End Sub
Aphelion propose 3 filtres de convolution passe-haut à travers les opérateurs ImgHighPass3×3,
ImgHighPass5×5 et ImgHighPass7×7.
Regarder leur définition et les comparer. Les appliquer à l'image "clocks",
calculer l'image de la différence des résultats deux à deux :
I1 = ImgHighPass3×3 − ImgHighPass5×5 I2 = ImgHighPass3×3 − ImgHighPass7×7 I3 = ImgHighPass5×5 − ImgHighPass7×7
Comparer qualitativement le comportement des trois filtres en fonction de I1, I2 et I3.

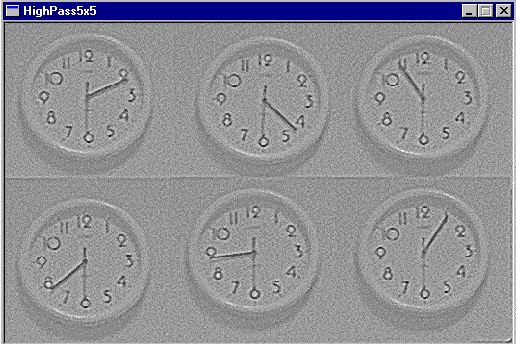

Voici les filtres HighPass 3×3, 5×5 et 7×7.
Ils travaillent donc sur des fenêtres de taille respectivement 3×3, 5×5, et 7×7.
On note une augmentation du bruit sur le 5×5 par rapport au 3×3, et sur le 7×7 par rapport au 5×5.



Voici :
I1 = 3×3 − 5×5 I2 = 3×3 − 7×7 I3 = 5×5 − 7×7
L'image I2 comporte beaucoup de détails, cela met en évidence l'écart de filtrage entre 3×3 et 7×7.
Les images I1 et I3 comportent en effet moins de détails ; cela est du à un faible écart de filtrage entre 3×3 − 5×5 et 5×5 − 7×7
Comparer les définitions des filtres ImgHighPassN×N et ImgLaplacianN×N. D'une façon générale. Comment peut-on définir la nature de la différence entre les 2 types de filtres ?
La somme des coefficients des filtres Laplaciens est nulle, alors que dans le cas des , elle fait 1.
Consulter la définition des filtres ImgLowPassN×N. Les appliquer à l'image "clocks". Appliquer le même traitement qu'en 7.



Voici les filtres LowPass 3×3, 5×5 et 7×7.
Ils travaillent donc sur des fenêtres de taille respectivement 3×3, 5×5, et 7×7.
Au plus la fenêtre est grande, au plus le résultat est flou, et au plus on supprime le bruit.



L'image I2 comporte beaucoup de détails, cela met en évidence l'écart de filtrage entre 3×3 et 7×7.
Les images I1 et I3 comportent en effet moins de détails ; cela est du à un faible écart de filtrage entre 3×3 − 5×5 et 5×5 − 7×7.
Générer sous PaintBrush une image composée de 2 rectangles, l'un gris clair, l'autre gris foncé. Sous Aphelion, lui ajouter un bruit uniforme dont l'amplitude de variation est égale à l'écart entre les deux niveaux de gris de l'image originale. Appliquer un des filtres passe-haut de la question 7. Proposer une séquence d'opérateurs pour retrouver le contour.




On constate qu'il est difficile avec ce genre de technique d'isoler précisément des contours bruités.
Pour limiter les effets de l'estimation du gradient dans les zones bruités, on cherche généralement à définir un filtre qui amplifie les fortes variations "globales" et atténue (lisse) les petites variations locales. Proposer un filtre 7×7 qui réponde à ces deux critères. Le tester.
|
Ce filtre permet en une seule opération de réaliser une amplification des fortes variations globales
et qui atténue les petites variations locales. Les résultats sont proches de ceux obtenus en deux étapes distinctes. |
Consulter la définition du filtre de Cany-Deriche tel qu'il est implémenté dans Aphelion.
On pourra en proposer une définition simplifiée.
Définir un masque 1×7 approximant le filtre de Cany-Deriche en f(-3), f(-2), f(-1), f(0), f(1), f(2) et f(3)
pour les valeurs suivantes de α : 0.5, 1 et 2.
Déterminer le rôle joué par alpha sur la définition du filtre.
Créer et appliquer le masque correspondant à α=1 sur l'image "clocks".
Calcul du masque :
| F(-3) | F(-2) | F(-1) | F(0) | F(1) | F(2) | F(3) |
| 0.17 | 0.19 | 0.16 | 0 | -0.16 | -0.19 | -0.17 |
| F(-3) | F(-2) | F(-1) | F(0) | F(1) | F(2) | F(3) |
| 0.16 | 0.29 | 0.40 | 0 | -0.40 | -0.29 | -0.16 |
| F(-3) | F(-2) | F(-1) | F(0) | F(1) | F(2) | F(3) |
| 0.04 | 0.20 | 0.75 | 0 | -0.75 | -0.20 | -0.04 |
On constate d'après les résultats des calculs que a influence la largeur du masque. C'est à dire que lorsque a est petit, les valeurs du masque décroissent lentement autour du centre. Alors que lorsque a est plus grand, les valeurs sont élevées au centre, et décroissent rapidement.