Projet de
simulation d'un réseau avec files d'attentes
IUP.GMI.3 Montpellier II

Introduction

Le projet consiste en la réalisation d'un simulateur et d'expériences pour étudier le comportement d'un réseau à commutation de paquets soumis à différentes conditions de trafic. On cherche en particulier à étudier l'influence de la distribution du temps de service d'une part, et de l'intensité des rafales d'autre part, sur le temps de réponse des paquets.

Sommaire

• Introduction
• Sommaire
• Description du réseau
• Architecture du simulateur
• Expérience 1
• Expérience 2
• Expérience 3
• Expérience 4
• Conclusion
• code source complet et rapport (zip 202Ko)

Description du réseau

Topologie 1 :

Les paquets suivent 6 routes numérotées de r₁ à r₆, et formées des suites de files d'attente suivantes :

• r₁ = (1,2,3)
• r₂ = (2,3,4)
• r₃ = (3,4,5)
• r₄ = (4,5,6)
• r₅ = (5,6,1)
• r₆ = (6,1,2)

Le débit moyen des paquets arrivant sur la route r_i est égal à λ_i = i × λ₀, où λ₀ est un paramètre qui varie selon les expériences.

Topologie 2 :

• Les paquets arrivent à l'un des 6 noeuds du réseau.
• À leur sortie, ils sont routés au hasard vers un des 5 autres, avec la même probabilité.
• Après avoir visité ce deuxième noeud, ils reviennent au noeud de départ.
• Enfin, ils sortent du réseau.

Le débit moyen des paquets arrivant au noeud numéro i est égal à λ_i = i × λ₀, où λ₀ est un paramètre qui varie selon les expériences.

Architecture du simulateur

Le simulateur est basé sur un échéancier ; c'est une file d'événements. Chaque événement possède une date plus un certain nombre d'attributs. Lorsqu'il est traité, un nouvel événement est éventuellement inséré plus tard dans l'échéancier. L'expérience se termine lorsqu'il n'y a plus d'événement dans l'échéancier.

Le simulateur a été écrit en C++. L'échéancier est une liste d'événements. Chaque événement possède :

• un numéro de file : numéro de la file dans laquelle l'événement à lieu.
• un identifiant : identifiant du paquet qui créé cet événement.
• un type : type d'événement (arrivée dans la file, départ de la file).
• une date : date de l'événement
• une source : numéro de la file par laquelle le paquet est entré dans la route.
• une date d'arrivée dans la route : date à laquelle le paquet est entré dans la route.
• une date d'arrivée dans la file : date à laquelle le paquet est arrivé dans la file.
• un indicateur de nouveauté : indique si le paquet vient d'arriver dans la route et n'a pas encore été routé.
• des pointeurs sur les événements précédents et suivants : pour gérer la liste.

Expérience 1

• Les paquets arrivent selon des processus de Poisson;
• Le temps de service des paquets dans chaque file d'attente est une durée aléatoire de distribution exponentielle de moyenne 1ms.
• Les durées de service d'un même paquet dans différentes files sont supposées être indépendantes.

Résultats :

• 10 000 clients par route
• 100 000 clients par route
• 1 000 000 clients par route

• On constate que le temps de réponse moyen dans les files est supérieur à la valeur théorique de 1.0.
  Cela est dû au fait qu'il y a des clients en attente. Lorsque le nombre de clients en attente augmente (ie: lorsque le débit d'arrivée augmente - λ plus grand -), le temps de réponse augmente aussi.
• Le nombre de clients traités par file est de exactement 3 fois le nombre de clients simulés par route dans le cas de la topologie 1. En effet, les clients passent par 3 files. Pour la topologie 2, le nombre de clients traités est aléatoire mais proche de celui de la topologie 1.
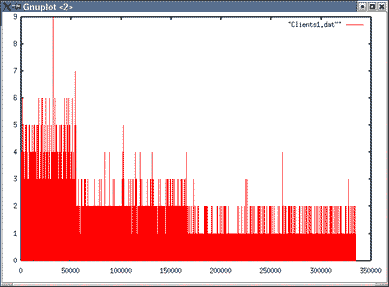
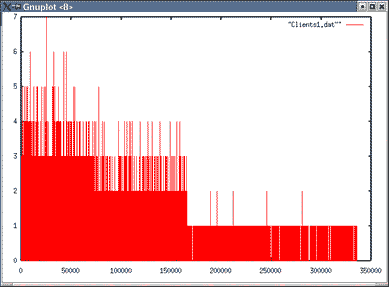
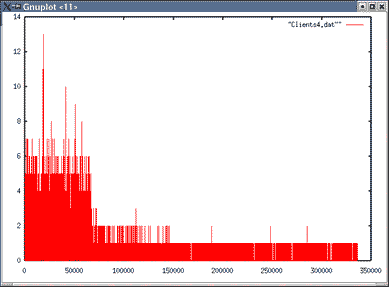
• On a vu que le nombre maximum de clients en attente augmente avec le débit d'arrivée. En topologie 1, on constate que la file pour laquelle il y a le moins de clients en attente est la file 3. En effet, Les files 1 et 2 subissent encore les débits importants de la file 6. Pour la topologie 2, on constate que le nombre maximum de clients en attente augmente avec le débit d'arrivée par file. Ainsi, il y a moins de clients en attente pour la file 1 que pour la file 6.
• Les probabilités que les temps de réponse par file dépassent un certain seuil augmente avec λ, mais dans cette expérience, même pour λ=0.06, on a une faible probabilité de dépasser 50ms.
• Les débits d'arrivées dans les routes sont proches de la théorie, soit i × λ₀.
• Les temps de réponse des routes sont proches de la somme des temps de réponse des 3 files empruntées.
• Les probabilités que les temps de réponse par route dépassent un certain seuil augmentent avec λ. La probabilité de dépassement augmente aussi avec le débit d'entrée dans la route, mais dans cette expérience, même pour λ=0.06, on a une faible probabilité de dépasser 50ms.

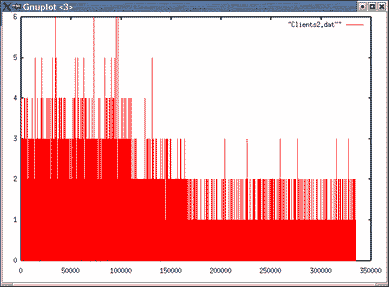
Images du nombre de clients en attente pour λ=0.03

Topologie 1 File 2	Topologie 1 File 3
Topologie 2 File 2	Topologie 2 File 5

Expérience 2

• Les paquets arrivent selon des processus périodiques de période t = 1ms, interrompus par des périodes <<off>>.
• La durée des périodes <<on>> est constante et vaut 20ms.
• La durée des périodes <<off>> est aléatoire, de distribution exponentielle dont la moyenne est calculée pour que le débit global soit celui spécifié par la topologie;
• Le temps de service des paquets dans chaque file d'attente est comme dans l'expérience 1.

Résultats :

• 10 000 clients par route
• 100 000 clients par route
• 1 000 000 clients par route

• Il a d'abord fallu calculer les durées moyennes des périodes off pour chacune des files afin de respecter le cahier des charges.
  (Nombre de clients par période <<on>> / (λ0 × n° de file)) - durée <<on>>
  soit (21 / (λ0 × n° de file)) - 20

  Durées moyennes théoriques des périodes <<off>> en fonction de la file et de λ

  λ \ file	1	2	3	4	5	6
  0.01	2080	1030	680	505	400	330
  0.02	1030	505	330	242.5	190	155
  0.03	680	330	213.333	155	120	96.6667
  0.04	505	242.5	155	111.25	85	67.5
  0.05	400	190	120	85	64	50
  0.06	330	155	96.6667	67.5	50	38.3333

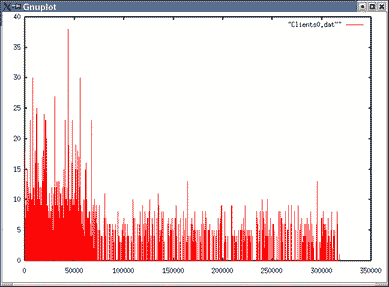
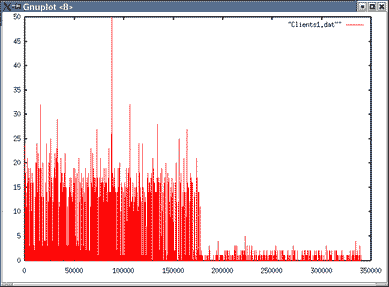
• L'introduction des périodes <<off>> augmente le temps de réponse des files et donc des routes. L'augmentation des temps de réponse est à peu prés constante quel que soit λ₀. Pour la topologie 2, les temps de réponse par file sont à peu prés 5 fois plus long que pour l'expérience 1 topologie 2. Mais pour la topologie 1, l'augmentation est plus forte pour les files à gros débit d'arrivée. (cf.tableau: un temps de réponse 2.65 fois plus long que dans l'expérience 1 pour la file 1, contre 3.6 fois plus long pour la file 6)

  Proportion d'augmentation du temps de réponse par file pour la topologie 1 par rapport à l'expérience 1

  file	1	2	3	4	5	6
  proportion d'augmentation	2,65	2,8	3,0	3,3	3,5	3,6

• L'augmentation du temps de réponse entraîne un plus grand nombre maximum de clients en attente.
• Les probabilités que les temps de réponse par file dépassent un certain seuil sont supérieures à l'expérience 1. Dès λ=0.02, on commence à avoir de faibles probabilités d'avoir un temps de réponse supérieur à 50ms.
• Les débits d'arrivées dans les routes sont à nouveau proches de la théorie, et similaires à l'expérience 1, ce qui était attendu par le calcul des durées <<off>>.
• L'augmentation du temps de réponse par route pour la topologie 1 est de environ 3 fois les temps de réponse par route de l'expérience 1 topologie 1. L'augmentation du temps de réponse par route pour la topologie 2 est de environ 5 fois les temps de réponse par route de l'expérience 1 topologie 2.
  Dans les deux topologies cela semble correct car les routes passent par des files dont les temps de réponse ont été augmentés en moyenne dans la même proportion.
• Les probabilités que les temps de réponse par route dépassent un certain seuil sont aussi augmentées par rapport à l'expérience 1. Dès λ=0.01, on a une probabilité non nulle d'avoir un temps de réponse supérieur à 50ms.

En résumé, les arrivées par vagues massives dues aux périodes <<on>><<off>> augmentent le nombre de clients en attente par file entraînant l'augmentation des temps de réponse.

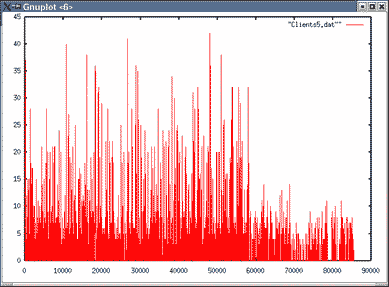
Images du nombre de clients en attente pour λ=0.03

Topologie 1 File 1	Topologie 1 File 6
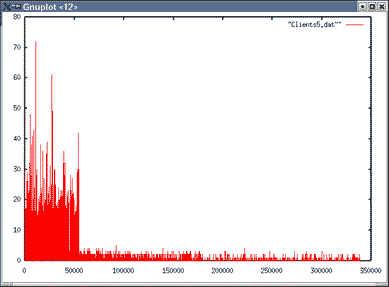
Topologie 2 File 2	Topologie 2 File 6

Expérience 3

• Les paquets arrivent comme dans l'expérience 2;
• Le temps de service des paquets dans chaque file d'attente est constant de durée 1ms.

Résultats :

• 10 000 clients par route
• 100 000 clients par route
• 1 000 000 clients par route

• Les résultats de l'expérience 3 sont proches de ceux de l'expérience 2.
• Néanmoins, on s'aperçoit que le nombre de clients en attente est sensiblement plus faible. Cela peut être dû au fait que le temps de traitement est constant, et identique aux inter-arrivées des paquets. Même en période <<on>>, la file d'attente se remplit peu.
• Cela entraîne une diminution sensible des temps de réponse par files et donc par routes.
• Les probabilités que les temps de réponse par file et par route dépassent un certain seuil sont donc moindres que pour l'expérience 2.

Images du nombre de clients en attente pour λ=0.03

Topologie 1 File 1	Topologie 1 File 6
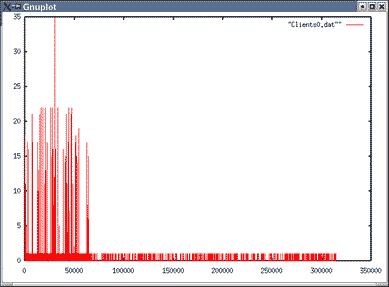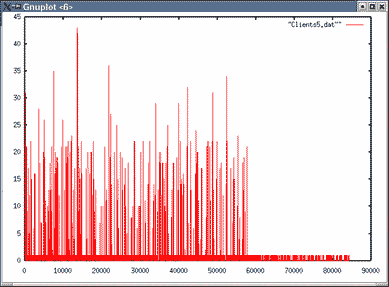Topologie 2 File 2	Topologie 2 File 6

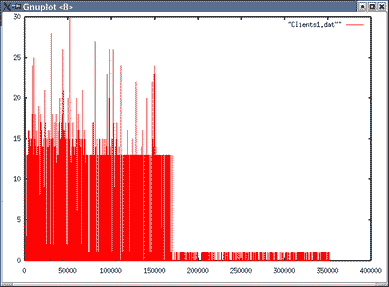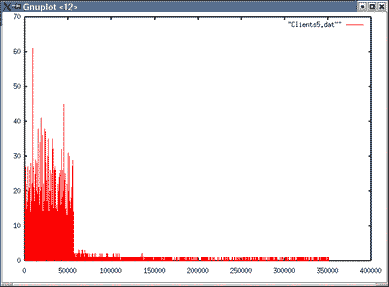Expérience 4

• Dans cette expérience, le réseau est comme dans l'expérience 3.
• Les files d'attente ont une capacité limitée à 100 paquets.
• Mesurer le taux de perte des paquets, pour chaque file d'attente et pour chaque route.

Résultats :

• 10 000 clients par route
• 100 000 clients par route
• 100 000 clients par route limite à 50 clients par file
• 1 000 000 clients par route

• Lorsqu'il n'y a pas de perte (ie: lorsque le nombre maximum de clients en attente est inférieur à 100), les chiffres sont très similaires à ceux de l'expérience 3.
• La perte de paquets entraîne la limite à 100 du nombre de clients en attente. Le temps de réponse des files et des routes s'en trouve diminué quand il y a eu des pertes, par rapport à l'expérience 3.
• Les probabilités de perte de paquets sont assez faibles. Ces probabilités sont plus fortes pour les files à forts débits d'arrivées, comme la file 6.

Images du nombre de clients en attente pour λ=0.06

	Topologie 1 File 6
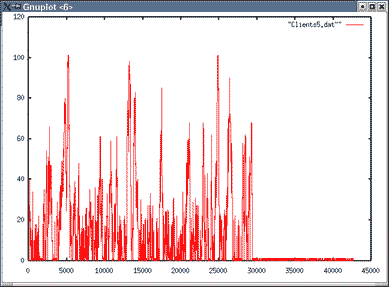Topologie 2 File 1	Topologie 2 File 6

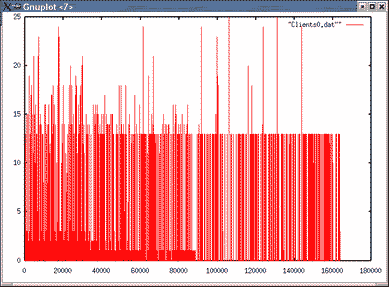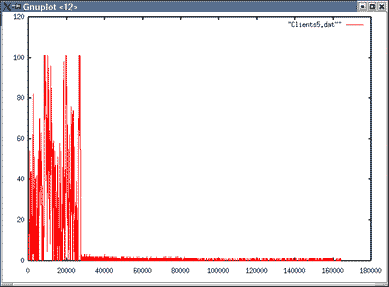Conclusion

La mise au point et l'implémentation d'un simulateur n'est pas évidente. Beaucoup d'erreurs peuvent se glisser dans les mesures sans qu'il soit aisé de les détecter.
L'échéancier mis en place est une méthode intéressante qui doit pouvoir être réutilisée dans d'autres types de simulations.
Ce projet nous a permis de vérifier expérimentalement les calculs théoriques vus en cours et de mieux juger de l'impact de la variation de certains paramètres.

Quitter