Rapport de stage sur: l'animation des graphes en Java

1.1 Situation de départ

M.Habib nous a transmis le projet des étudiants du T.E.R de maîtrise.
Ce logiciel permettait de représenter graphiquement des algorithmes de parcours de graphe (Dijkstra, lexicographique, A*, A, largeur).
Le projet permettait déjà de sauvegarder et d'afficher les différentes étapes des algorithmes ainsi que de les stocker sur fichier au format XML en utilisant un package spécialisé (Xerces).
Bien que fonctionnel ce projet comportait un certain nombre de problèmes dont certains se sont révélés lors des tests sur d'autres plateformes.
A savoir :

• La gestion des événements de souris ne permettait pas de sélectionner convenablement les différentes options proposées.
• La boîte d'ouverture des fichiers ne permettait pas d'accéder au répertoire de son choix.
• Le redimensionnement de la fenêtre d'affichage ne se faisait pas convenablement et n'affichait qu'une partie des graphes.
• Plus un ensemble de bogues survenant lors d'utilisations moins courantes.

1.2 Solutions possibles

Nous avons commencé par hésiter à recommencer le projet dans son intégralité au vu de la difficulté de compréhension des sources qui ne disposaient d'aucun commentaire.
Mais cela nécessitait un gros travail supplémentaire par rapport au sujet demandé.

1.3 Outils à disposition

Nous disposons du Jdk sur les machines de la faculté. N'ayant pas d'environnement de développement, il était difficile de déboguer et de naviguer dans les classes pour comprendre les sources du T.E.R maîtrise.
Nous avons donc travaillé essentiellement sur nos machines personnelles avec JBuilder 4 sous Windows.

1.4 Solutions choisies

Nous avons finalement opté pour une amélioration du projet existant.
Pour ce faire nous avons tout d'abord travaillé ensemble sur la compréhension des sources, ainsi que sur la mise à jour des structures de données.
Afin de mieux saisir le fonctionnement du logiciel nous avons développé un premier algorithme simple : la coloration d'un graphe.
Nous avons ensuite opté pour une séparation des tâches afin de réaliser les algorithmes de couplage et de flot.

2.1 Evolution de la structure de données du logiciel

La structure de données permettait déjà de stocker le poids d'une arête mais ne permettait pas le stockage du flot.
Nous avons donc rajouté la possibilité de conserver le flot et nous avons utilisé le poids comme capacité.
Il a fallu modifier certaines classes pour y ajouter les attributs correspondants et leurs accesseurs.
Il nous a également fallu modifier bon nombre de méthodes notamment les constructeurs par copie.
Le package Xerces (de Apache et W3C) servant à gérer la sauvegarde sur fichier XML étant énorme (plus de 1,6Mo), un nouveau package a été développé pour le remplacer.

2.2 Algorithme de coloration

Nous avons réalisé cet algorithme en commun afin de nous familiariser avec l'utilisation et l'implémentation du logiciel.
Voir le projet Algorithmique Distribuée Parallèle k-coloration pour plus de détails sur la coloration.

• 2.2.1 Problème rencontré

  Les algorithmes implémentés par les étudiants de maîtrise utilisent des graphes orientés.
  Or l'algorithme de coloration s'applique à des graphes non orientés.
  Il nous a donc fallu, pour que chaque sommet connaisse ses successeurs ainsi que ses prédécesseurs, construire les arcs dans les deux sens.
  Cependant nous n'affichons qu'une seule arête pour une meilleure lecture du graphe.

  Sommaire

• 2.2.2 Algorithme

  Données : graphe non orienté G=(X,E)
  Résultat : une coloration du graphe : chaque sommet est coloré différemment de ses voisins

      Début :
        pour tous les sommets x de X faire
          coloration(x)=0;
        fpr
        int modif=1;
        pour tous les sommets x de X faire
          coloration(x)=1;
          tant que (modif != 0) faire
            modif=0;
            pour tous les successeurs y de x faire
              si (coloration(x) = coloration(y)) alors
                coloration(x)++;
                modif++;
              fsi
            fpr
          ftq
        fpr
      Fin
     

  Remarque: cet algorithme ne donne pas toujours le nombre minimal de couleurs nécessaires pour colorer l'ensemble des sommets.
  Il donne toute fois un résultat relativement satisfaisant compte tenu qu'il n'existe aucun algorithme simple donnant la coloration minimale dans tous les cas.

  Sommaire

• 2.2.3 Représentation graphique des étapes de l'algorithme

  Le sommet exploré est coloré en bleu et les arêtes vers tous ses successeurs sont colorées en blanc.

  

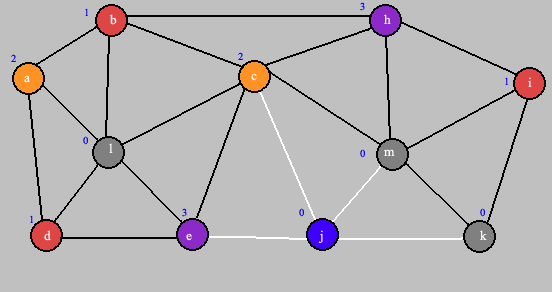
  On affecte à ce sommet la plus petite couleur non utilisée par un de ses voisins.

  

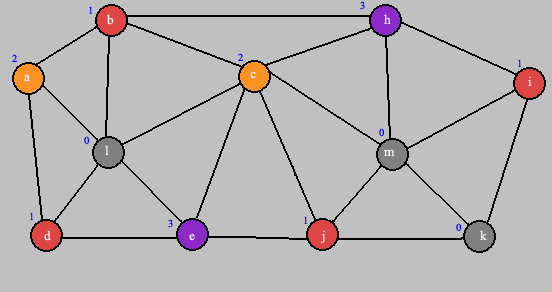
  On remet en noir les arêtes. Et on fait de même pour tous les sommets du graphe.

  Sommaire

2.3 Algorithme de Ford Fulkerson

Ford et Fulkerson ont proposé le premier et le plus simple des algorithmes pour le flot max dans un réseaux de transport G=(X, A, C, s, t).
Il est basé sur la recherche de chemins successif dans le graphe d'écart ou, ce qui revient au même, de chaîne améliorante successive dans le graphe d'origine.

• 2.3.1 Problème rencontré

  Etant donné que nous n'avions pas accès aux prédécesseurs, il a fallu tester les arcs dans l'autre sens.

• 2.3.2 Algorithme

  L'algorithme de FF travaille directement sur le graphe d'origine et explore virtuellement le graphe d'écart.
  Chaque itération a pour but la recherche d'une chaîne améliorante de s à t dans G, ou donc d'un chemin dans Ge.
  Si on trouve une telle chaîne on calcule l'augmentation de flot qu'elle permet. C'est le minimum des capacités résiduelles des arcs de la chaîne.
  On peut alors augmenter le flux de unités sur les arcs avant de et le diminuer sur les arcs arrières.
  L'algorithme se termine lorsqu'on ne trouve plus de chaîne améliorante.

  Données : graphe non orienté G=(X,E)
  Résultat : une coloration du graphe : chaque sommet est coloré différemment de ses voisins

      Début :
        Construire le graphe d'écart Ge
        Tant que chemin améliorant sur Ge
          Construire le graphe d'écart Ge
          Chercher un chemin améliorant sur Ge
          Si chemin améliorant sur Ge
            δ = le minimum des arcs du chemin sur Ge
            améliorer de δ les arcs avant sur la chaîne de G correspondant au chemin dans Ge
            diminuer de δ les arcs avant sur la chaîne de G correspondant au chemin dans Ge
          Fin si
        Fin tant que
      Fin
     

  Sommaire

• 2.3.3 Représentation graphique des étapes de l'algorithme

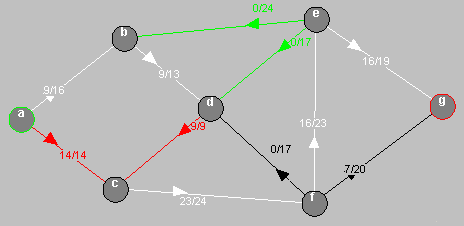
  Recherche d'une chaîne améliorante en bleue dans le graphe de départ, s est en vert et p en rouge.

  

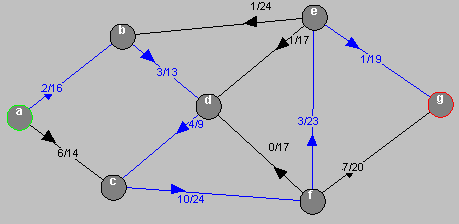
  Amélioration du flot sur la chaîne trouvée, les arcs saturés sont en rouge et les arcs améliorés en blanc.

  

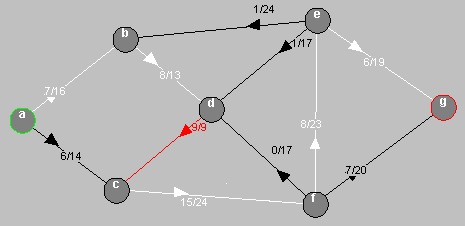
  Amélioration d'une chaîne contenant des arcs dans le sens inverse, les arcs diminués sont en vert pomme et les arcs diminué à 0 sont en vert fluo.

  
  Sommaire

2.4 Algorithme de couplage max sur un graphe biparti

L'algorithme de couplage comme celui de coloration s'applique à des graphes non orientés. Nous construisons donc les exemples avec des graphes aller-retour et n'affichons qu'une seule arête. Cet algorithme ne s'applique qu'à des graphes particuliers : les graphes bipartis. Il faut donc respecter cette contrainte lors de la création d'exemples.

• 2.4.1 L'algorithme

  Donnée : Un graphe biparti G = (X, Y, E)
  Résultat : un couplage maximal

      Début :
        couplage =Ø
        pour tous sommets x de X Y faire
          si x non marqué alors
            tant que voisin(x) est marqué faire
              choisir un autre voisin de x
            ftq
            si il existe un voisin de x non marqué alors
              on marque ce voisin
              couplage = couplage U {x voisin(x)}
            fsi
          fsi
        fpr
  
        à ce stade de l'algorithme on a un couplage "simple"
        on va maintenant chercher les chaînes alternées améliorantes
  
        tant que couplage non max
          pour tous sommets x non marqué faire
            chaine_alternee_ameliorante = améliorer(x);
            amélioration du couplage;
          fpr
        ftq
      Fin
  
  
      Améliorer(chaîne)
      Données: une chaîne de départ, le graphe G muni d'un couplage
      Résultat: une chaîne alternée améliorante
  
      Début
        On récupère le dernier sommet z de la chaîne passée en paramètre.
        pour tous les voisins y de z faire
          si y non marqué alors
            chaîne_alternée = chaîne + y;
            marque y;
            marque z;
          sinon
            on récupère dans le couplage le voisin t de y;
            Améliorer(chaîne+ y + t);
          fsi
        fpr
      Fin
     

  Sommaire

• 2.4.2 Représentation graphique des étapes de l'algorithme

  Affichage du couplage simple: les sommets marqués en bleu et les arêtes du couplage en blanc.

  

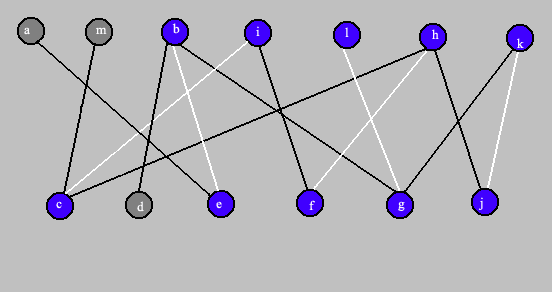
  Recherche d'une chaîne alternée améliorante. Modification du couplage: on affiche en mauve les arêtes qui vont être supprimées du couplage et les sommets affectés par cette modification. Et on affiche en vert les arêtes qui améliorent le couplage.

  

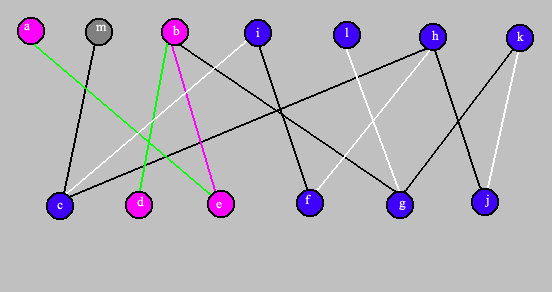
  Finalement on affiche en blanc les arêtes faisant partie du couplage maximal. Les sommets et les arêtes affectés par les modifications restent en mauve.

  
  Sommaire

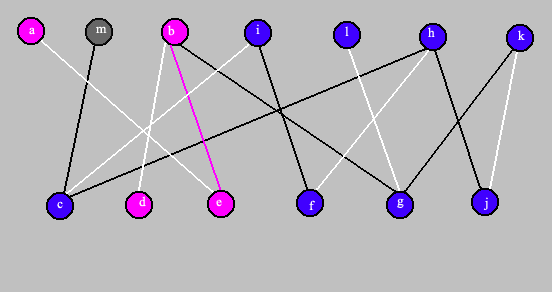
2.5 Package XML

De même que le package Xerces, le nouveau package permet la lecture et l'écriture au format XML 1.0.
Il détecte les erreurs en précisant la ligne et le type d'erreur.
Il utilise une structure de données efficace avec des tables de hachage pour gérer les propriétés des éléments XML, ainsi que les familles de sous-éléments.
La taille finale est de 9Ko, le gain est donc appréciable (200 fois plus petit).

3.1 Passage du programme à l'applet Java

Afin de mettre le programme en ligne, des modifications s'imposent, il faut soit utiliser le plugin Java pour les navigateurs, soit transformer le code pour qu'il respecte le Java1.1.
Dans tous les cas il faut transformer les entrées sorties Java en autant de connexions avec le serveur.

3.2 Optimisation de la structure de donnée

Les structures de données n'ont pas été faites dans un souci d'optimisation, une évolution souhaitable serait de limiter les comparaisons de chaîne ainsi que les parcours.

3.3 Implémentation de nouveaux algorithmes

L'algorithme de Ford Fulkerson pourrait être amélioré si pour chaque graphe d'écart on prenait le chemin améliorant le plus court (algorithme Edmonds Karp).