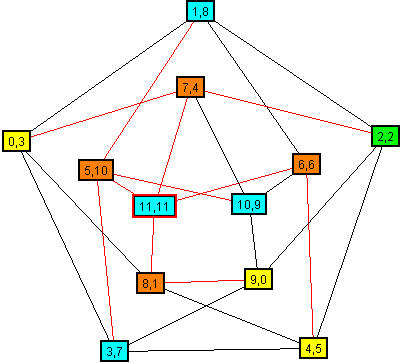
Un graphe 4-coloré proposé par M.Chvatal
Le projet d'algorithmique distribuée de maîtrise IUP GMI
consiste en l'amélioration d'un algorithme de k-coloration distribuée.
Le problème de coloration est un problème difficile (np-complet).
Sa distribution sur plusieurs processeurs est tout aussi difficile (ex: plusieurs machines en réseau).
La coloration d'un graphe consiste à donner une couleur à tous les sommets,
de telle manière que deux sommets voisins (reliés par un arc) ne possèdent pas la même couleur.
Le nombre chromatique d'un graphe est le nombre minimal de couleurs nécessaire pour le colorer.
Un graphe donné est k-colorable, si k est supérieur ou égal au nombre chromatique du graphe.
Une k-coloration consiste à colorer le graphe avec k couleurs différentes ou moins, ou dire que c'est impossible.
Voir la partie coloration, du projet d'animation des graphes en Java.

La distribution d'un algorithme consiste à faire une partie de l'exécution de l'algorithme sur différents processeurs distants communiquants entre eux. Le but est en général de pouvoir attaquer des problèmes trop gros ou trop longs pour être traités sur une même machine.
Nous nous intéresserons au cas où les processeurs sont sur plusieurs machines communiquant par échange de message en réseau. Sur la figure ci-dessus chaque sommet exécute l'algorithme. L'algorithme exécuté est identique sur chaque sommet.
Une exécution est dite parallèle lorsque plusieurs algorithmes s'exécutent simultanément, contrairement à une exécution distribuée séquentielle où chaque sommet exécute son algorithme à son tour.
Le développement doit se faire en plusieurs parties, afin de pouvoir constater les gains des méthodes plus efficaces.
Le back-track distribué séquentiel est la méthode de coloration de référence.
Il s'agit d'une coloration classique similaire à un algorithme non distribué.
Il sera détaillé plus tard.
C'est le sujet principal. Il s'agit de trouver une méthode permettant d'améliorer la vitesse de coloration grâce au parallélisme. Chaque sommet étant géré par un processus différent, plusieurs sommets peuvent travailler et communiquer simultanément.
L'implémentation peut se faire sur une seule machine (avec plusieurs processus ou threads), dans un langage quelconque. Les sommets doivent communiquer par un système FIFO (sockets, tubes, ou autres).
Afin de gérer l'exécution distribuée (parallèle) des différents sommets, nous utilisons des threads. Le programme final tournant sur une machine mono-processeur, un ordonnanceur distribue du temps de calcul à chacun des threads de manière équitable en fonction de leurs priorités.
L'ensemble de la programmation a été faite en Java (1.4).
C'est donc la machine virtuelle Java qui tient le rôle de l'ordonnanceur des threads.
Le choix s'est porté sur Java pour la facilité de mise en oeuvre des algorithmes et
des structures de données, ainsi que pour la richesse de sa bibliothèque (communication,
graphisme, ...).
La vitesse d'exécution s'est révélée très satisfaisante par rapport aux implémentations en C
avec des fonctions systèmes Linux (On arrive à colorer jusqu'à 2000 sommets -
1% d'arcs - en moins de 10 secondes).
Les différents sommets ne communiquent entre eux que par l'envoie de messages qui
sont transmis dans des canaux de communication FIFO.
Ces canaux de communication ont été réimplémentés pour des raisons de performance et de simplicité :
Les messages transmis sont des objets (pas de besoin de parsing) ; ils sont stockés dans une file illimitée.
La synchronisation de ces files pour l'utilisation simultanée par plusieurs threads est assurée.
La programmation des sommets a été divisée en classes : une par algorithme. Il est ainsi aisé d'ajouter, modifier ou supprimer des algorithmes. Cela évite aussi les confusions entre les types de messages échangés.
La coloration ne peut pas se faire sans préambule. Plusieurs algorithmes précèdent le début de la coloration.
Le premier algorithme lancé est une élection.
Elle est destinée à élire un sommet qui centralisera certaines réponses comme la fin de la coloration.
Plusieurs sommets peuvent démarrer la coloration simultanément.
La politique est d'élire le sommet qui a le plus de voisins et en cas d'égalité celui de plus fort identifiant.
L'élu lance ensuite un arbre couvrant dont il est la racine.
Chaque sommet propose sa paternité à tous ses voisins.
Un sommet devient fils du premier sommet dont il reçoit l'offre de paternité.
Puis une numérotation en profondeur est lancée sur l'arbre couvrant.
Une fois la numérotation terminée, une méthode de coloration est lancée par l'élu.
Le back-track distribué séquentiel fonctionne comme un back-track local.
Les sommets se colorent dans l'ordre de leur numérotation en profondeur,
en tenant compte de la couleur de leurs voisins déjà colorés.
Si un sommet n'arrive pas à se colorer, il envoie un message au sommet précédant
lui demandant de tester une autre couleur.
Si l'élu reçoit une demande de changement de couleur, c'est que la coloration est impossible.
Si le dernier sommet arrive à se colorer, la coloration est terminée et réussie.
L'idée de cette amélioration réside dans le fait qu'il est souvent
inutile de remonter au sommet précédant (dans l'ordre du back-track).
En effet, si un sommet n'arrive pas à se colorer,
il faut que ce soit un de ses voisins qui change de couleur pour éventuellement le débloquer.
Ici, le back-track fait remonter l'erreur au plus petit voisin supérieur au sommet.
Le nombre de back-tracks est considérablement réduit.
Un des intérêts du distribué est que l'exécution peut se faire de manière parallèle.
L'avantage est que le temps de calcul est d'autant diminué.
Nous avons essayé de mettre cette idée en pratique.
En plus du back-track séquentiel amélioré, nous avons mis en place une coloration secondaire parallèle.
Cette coloration secondaire fait des essais de coloration sans interférer avec la coloration back-track principale.
Ainsi, la coloration secondaire fait souvent plusieurs essais et même des back-tracks.
Aussi lorsque la coloration principale arrive sur un sommet,
la couleur fournie par la coloration secondaire est testée en premier.
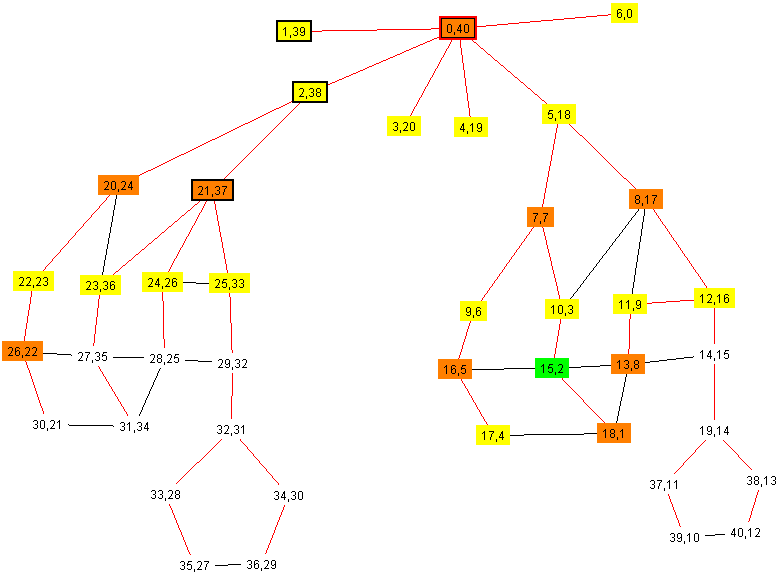
On voit sur cette exécution la coloration primaire (sommets entouré en gras),
et les colorations secondaires (sommets colorés non entourés).
Sur un graphe peu connexe k-colorable, la coloration principale prend directement la bonne couleur.
Plusieurs idées intéressantes auraient mérité d'être développées. Notons par exemple la détection des composantes connexes colorable indépendamment.
Pour faire une estimation du gain du parallélisme, une idée était de faire une exécution par cliquets :
Cela permet mesurer le temps d'exécution en nombre de clics, et de faire des comparaisons entre du séquentiel et du parallèle. Cela ne permet cependant pas de traiter les écarts de transmission et autres problèmes de synchronisation. Ce n'est donc pas une mesure mais une estimation.
Une amélioration supplémentaire serait de mettre en place un processus superviseur pour détecter la terminaison de la coloration. En effet, la coloration secondaire se fini souvent trés vite, et la terminaison arrive bien aprés, lorsque la coloration principale se termine.
Les principaux algorithmes de résolution pour le problème de k-coloration partagent
une caractéristique : l'ajout avant ou durant la recherche, de liens entre des sommets du graphe auparavant
non connectés. L'algorithme Dynamic Backtracking (Bessière, Maestre, Meseguer) présente une nouvelle méthode
sans ajout de liens entre les différents sommets.
Cet algorithme utilise certaines des bonnes propriétés de la version centralisée de dynamic backtraking.
Il assure la complétude de la recherche, et autorise un haut niveau
d'asynchronisme en évitant l'ajout de liens superflus.
Le principe de cet algorithme repose sur l'envoie de nogood, ce sont des messages qui contiennent le contexte d'un
sommet du graphe. L'interprétation de ces nogoods permet d'obtenir la coloration.
Le but de cet algorithme est de garder le meilleur d'ABT et DiBT : l'idée des nogoods provient d'ABT et la
volonté de ne pas relier des sommets non connectées provient de DiBT.
Cet algorithme correspondait exactement à nos besoins mais sa complexité ne nous permettait pas de
l'implémenter dans le temps imparti.
De plus cet algorithme a besoin d'un processus superviseur pour détecter la terminaison, ce qui était un peu en
contradiction avec notre cahier des charges.
Il aurait été intéressant d'implémenter les algorithmes sur plusieurs machines en réseau,
mais le manque de temps nous en a empêché.
Cela aurait eu plusieurs avantages :
La coloration est un sujet difficile, la distribution aussi.
Nous avons néanmoins une solution relativement performante.
Du temps supplémentaire aurait été nécessaire pour implémenter et tester nos autres idées.